Imagine you’re on a scenic hike, traversing a winding mountain path. As you climb, the air gets thinner, the temperature drops, and the landscape changes dramatically. The journey itself is exciting, but what if you could quantify the overall change in elevation, the total impact of the varying terrain, and even predict your final altitude? This is precisely what the Fundamental Theorem of Line Integrals allows us to do – it provides a powerful framework for understanding and calculating the cumulative effects of a path taken, whether it’s a physical journey or an abstract mathematical one.

Image: www.chegg.com
The Fundamental Theorem of Line Integrals, a cornerstone of vector calculus, connects the seemingly disparate worlds of line integrals and potential functions. It unveils a hidden relationship between the work done by a force field along a curve and the change in a potential function associated with that field. This powerful theorem offers a shortcut to calculating intricate line integrals, reducing complex calculations to simple evaluations of potential functions at the endpoints of the path.
A Journey Through Time: Tracing the Origins of the Fundamental Theorem
The history of the Fundamental Theorem of Line Integrals intertwines with the development of calculus itself. In the 17th century, Isaac Newton and Gottfried Wilhelm Leibniz laid the groundwork for the study of change and motion, with their groundbreaking work on derivatives and integrals. These concepts paved the way for the development of vector calculus, which delves into the realm of multi-dimensional spaces and the interplay of vector fields, curves, and surfaces.
The Fundamental Theorem of Line Integrals, in its full glory, emerged from the contributions of numerous mathematicians over centuries. The work of Augustin-Louis Cauchy, Bernhard Riemann, and others laid the foundation for understanding the relationship between integration and differentiation in higher dimensions. The theorem itself, as we know it today, is often credited to the insightful work of physicist and mathematician Hermann von Helmholtz, who, in the 19th century, formulated a crucial connection between the potential energy of a system and the work done by forces acting upon it.
Deciphering the Fundamental Theorem: A Breakdown
At its core, the Fundamental Theorem of Line Integrals states that the line integral of a conservative vector field along a path depends only on the starting and ending points of that path. It elegantly connects line integrals, which measure the work done by a force along a curve, with potential functions, which represent the potential energy associated with that force.
Let’s dissect this theorem step by step:
Conservative Vector Fields: A conservative vector field possesses the crucial property of being path-independent. This means that the work done by the field in moving an object from one point to another is independent of the specific path taken. In essence, a conservative field is governed by the concept of potential energy – the work done against the field can be stored as potential energy, ready to be released later.
Potential Functions: Associated with each conservative vector field is a potential function, whose gradient gives the vector field itself. Think of a potential function as a “landscape” where the gradient represents the steepness or direction of the terrain. The value of the potential function at a specific point represents the potential energy associated with that point.
Line Integrals: A line integral, in its essence, measures the work done by a force field along a curve. It takes into account both the force acting on the object and the distance traveled along the curve. The Fundamental Theorem of Line Integrals connects this concept of work with the notion of potential energy.
The Theorem’s Power: The Fundamental Theorem allows us to bypass the complex task of calculating line integrals directly. Instead, it enables us to evaluate the potential function at the endpoints of the path and take the difference, thus elegantly calculating the line integral with a simple subtraction.
Unlocking the Secrets of Line Integrals: Applications in Real-World Contexts
The Fundamental Theorem of Line Integrals finds applications in various scientific and engineering disciplines. Here are a few examples:
Physics: In mechanics, the theorem is used to calculate the work done by a conservative force, such as gravity or the elastic force of a spring. It provides a convenient method for analyzing the motion of objects under the influence of these forces.
Fluid Mechanics: The theorem plays a crucial role in understanding the flow of fluids and the forces acting on objects submerged in them. For example, it is used to analyze the work done by the pressure forces exerted by fluids on submerged bodies.
Electrostatics: In electromagnetism, the fundamental theorem is used to calculate the electric potential difference between two points in an electric field. This potential difference is directly related to the work done by the electric field in moving a charge between those points.
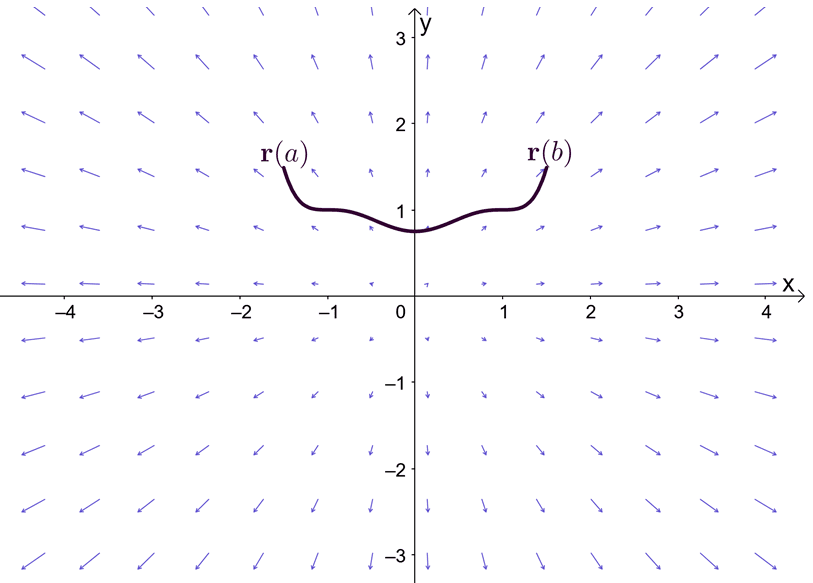
Image: www.storyofmathematics.com
Expert Insights and Practical Tips: Navigating the World of Line Integrals
- Visualizing is Key: When working with the Fundamental Theorem of Line Integrals, it’s crucial to visualize the vector field, the path, and the potential function associated with the field. This visual understanding can greatly enhance comprehension and simplify the problem-solving process.
- Understanding the Essence: Remember that the Fundamental Theorem of Line Integrals is a tool for understanding the relationship between force fields, paths, and potential functions. It offers a way to circumvent complex calculations by leveraging the concept of potential energy.
- Don’t Fear the Math: While the theorem can be initially daunting, it becomes much clearer with practice. Familiarize yourself with the concepts of conservative vector fields, potential functions, and line integrals, and explore applications through problem-solving exercises.
Fundamental Theorem Of Line Integrals
Conclusion: Embracing the Power of the Fundamental Theorem
The Fundamental Theorem of Line Integrals is a remarkable tool that simplifies and enhances our understanding of line integrals. By connecting line integrals with potential functions, it offers a shortcut for calculating the work done by a force field along a path, allowing us to delve into deeper insights about the world around us. Whether you are a student of mathematics, a scientist, or simply someone curious about the hidden connections within our universe, the Fundamental Theorem of Line Integrals offers a powerful lens through which to explore and understand the profound interplay of forces, paths, and potential. Now, armed with this knowledge, embark on your own journey of discovery – explore the fascinating world of line integrals and uncover their profound connections to the forces and landscapes that shape our reality.






