Have you ever stopped to wonder about the hidden secrets nestled within the seemingly mundane number 69? It’s a number that often evokes laughter or a mischievous grin, but beneath the surface lies a fascinating world of mathematical principles and intriguing patterns. This exploration delves into the realm of factors, those numerical building blocks that form the very foundation of 69. We’ll uncover how these factors come together, their role in mathematical calculations, and the surprising connections they reveal.

Image: www.researchgate.net
Factors, simply put, are numbers that divide evenly into a given number, leaving no remainder. In the case of 69, discovering its factors might seem like a straightforward task, but the process reveals surprising insights about the nature of numbers themselves. By unraveling the factors of 69, we’ll embark on a journey into the heart of mathematics, unlocking hidden patterns and learning how factors influence the world around us.
Finding the Factors of 69: A Step-by-Step Approach
Let’s dissect the number 69 and uncover its factors. To embark on this journey, we’ll start with the basics:
-
Prime Factorization: The first step is to break down 69 into its prime factors, which are numbers greater than 1 that are only divisible by 1 and themselves. 69 is not a prime number, but it can be factored into 3 and 23. Both 3 and 23 are prime numbers, meaning they cannot be factored further. We can express this prime factorization as 69 = 3 x 23.
-
Listing the Factors: Now that we have the prime factorization, we can systematically find all the factors of 69. To do this, we need to consider all possible combinations of its prime factors:
- 1 (which is always a factor of any number)
- 3 (one of the prime factors)
- 23 (the other prime factor)
- 3 x 23 = 69
Therefore, the factors of 69 are: 1, 3, 23, and 69. Notice that the number of factors, in this case, is 4.
Exploring the World of Factors: Applications and Significance
The seemingly simple process of finding factors has a remarkable impact in various fields. Here are some key applications:
-
Understanding divisibility rules: Understanding factors helps us understand divisibility rules, which are shortcuts to quickly determine if one number is divisible by another. For instance, knowing that 69 is divisible by 3 is a direct consequence of the fact that 3 is one of its factors.
-
Simplifying Fractions: In mathematics, factoring is used to simplify fractions. For example, if we have the fraction 69/93, by factoring both the numerator and denominator, we can reduce it to 3/13, which is a simpler representation of the same value.
-
Solving algebraic equations: Factoring is an essential tool in solving algebraic equations. By factoring expressions, we can rewrite them in a simpler form, making it easier to find solutions.
-
Generating unique numbers: Factors are crucial in cryptography and encryption, where secure codes are created using unique numbers. Factoring large numbers into their prime factors is a fundamental process in modern cryptography.
Factorial Fun: Unveiling the Essence of Factorial Numbers
In the realm of mathematics, factorials embrace the power of factors in a unique way. A factorial of a non-negative integer n, denoted by n! is the product of all positive integers less than or equal to n. For instance, 5! = 5 x 4 x 3 x 2 x 1 = 120.
Factorials play a critical role in probability, statistics, and combinatorics. They allow us to understand the number of ways to arrange objects, such as the number of possible outcomes in a lottery or the number of seating arrangements in a room.
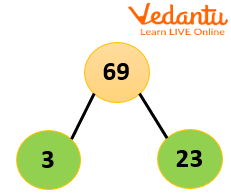
Image: www.vedantu.com
The Fascinating World of Perfect Numbers: Exploring a Mathematical Mystery
A perfect number is a positive integer that is equal to the sum of its proper divisors, which are all the divisors of a number excluding the number itself. For instance, 6 is a perfect number because its proper divisors are 1, 2, and 3, and 1 + 2 + 3 = 6.
Understanding the relationship between factors and perfect numbers is a fascinating journey. Perfect numbers have intrigued mathematicians for millennia, and their discovery has led to advancements in the field. Currently, mathematicians have only identified a finite number of perfect numbers, and the search for new ones continues.
Factors in Our Daily Lives: Unveiling Surprising Applications
While factors might seem like a purely mathematical concept, they have a surprisingly pervasive impact on our everyday lives. Every time we divide a pizza among friends or measure ingredients for a recipe, we are subconsciously utilizing our understanding of factors.
Think about the practical examples:
-
Division of food: When dividing a pizza into equal slices, we are essentially considering the factors of the total number of slices. For example, a 12-slice pizza can be divided equally among 2, 3, 4, 6, or 12 people.
-
Recipe ingredients: Recipes often require precise ingredient measurements, which involve understanding ratios and the relationship between ingredients. These ratios involve factors, as they represent the relationships between the quantities of different components in a recipe.
Factoring: A Gateway to Mathematical Discovery
Unlocking the secrets of factors opens a gateway to a deeper understanding of the mathematical world. By exploring their influence on numbers, we gain insights into the building blocks of our universe. From the intricacies of prime factorization to the elegant simplicity of divisibility rules, factors provide a lens through which we can view the interconnectedness of mathematical concepts.
Factors Of 69
Final Thoughts: Embracing the Power of Factors
As we journey through the realm of factors, we uncover a captivating tapestry of mathematical principles interwoven into the fabric of our existence. Factors are not just abstract concepts but fundamental tools that empower us to navigate the complex world of numbers.
Embrace the power of factors – they hold the key to unlocking mathematical secrets, simplifying everyday tasks, and deepening our appreciation for the intricate tapestry of our mathematical universe.






