Have you ever stopped to think about the numbers that perfectly divide into another number, leaving no remainder? These hidden companions, the factors of a number, hold a fascinating power in the world of mathematics. Today, we embark on a journey to explore the factors of 126, unraveling the secrets that lie within its numerical composition.

Image: www.cuemath.com
Understanding factors is not just a mathematical exercise. It’s a fundamental concept that forms the basis for numerous mathematical operations, such as finding the greatest common divisor (GCD) and the least common multiple (LCM). Factorization also plays a crucial role in fields like cryptography, where it’s used to secure sensitive data. In this article, we’ll explore the factors of 126, delve into their significance, and discover how they contribute to the wider mathematical landscape.
Defining Factors: Unveiling the Multiplicative Roots
Before diving into the factors of 126, let’s establish a clear definition. A factor of a number is any whole number that divides evenly into that number, leaving no remainder. It’s like finding the building blocks of a number, the smaller components that multiply together to form the original number.
Discovering the Factors of 126: A Number’s DNA
Now, let’s turn our attention to the number 126. To find its factors, we can systematically check each whole number from 1 up to 126, looking for those that divide evenly. However, there’s a simpler method: the process of prime factorization.
Prime Factorization: The Foundation of Factor Discovery
Prime factorization is like breaking down a number into its fundamental building blocks – prime numbers. A prime number is a whole number greater than 1 that is only divisible by 1 and itself. Think of prime numbers as the atoms of the number world.
To find the prime factors of 126, we can start by dividing it by the smallest prime number, 2. We get:
126 ÷ 2 = 63
Now, 63 is not a prime number, so we continue factoring:
63 ÷ 3 = 21
Again, 21 is not a prime number, so we continue:
21 ÷ 3 = 7
Finally, we’ve reached a prime number: 7. Therefore, the prime factorization of 126 is:
126 = 2 × 3 × 3 × 7
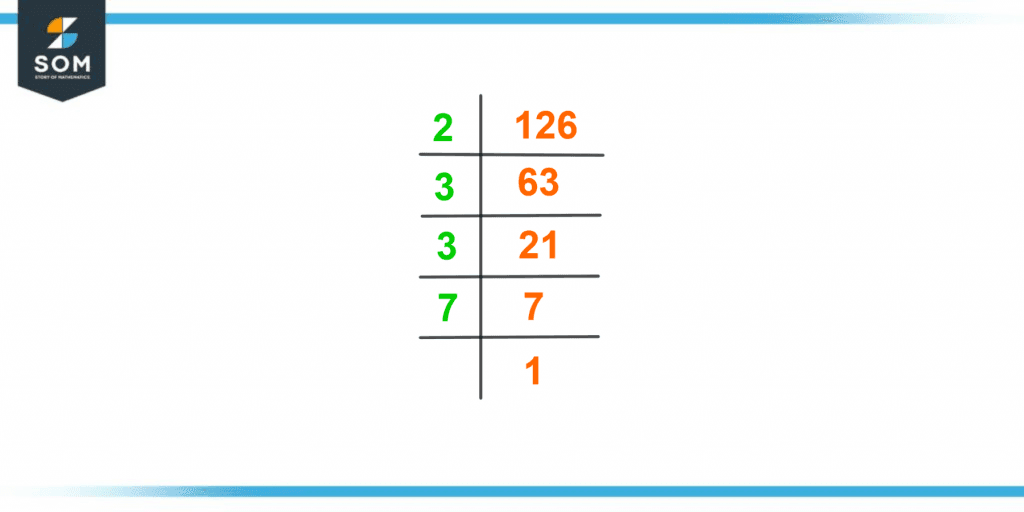
Image: betebt.com
Factors from Prime Factorization: Building Combinations
With the prime factorization of 126, we can easily determine all its factors. We simply consider all possible combinations of its prime factors. This includes:
- 1 (obtained by multiplying no prime factors)
- 2
- 3
- 3 × 3 = 9
- 2 × 3 = 6
- 2 × 3 × 3 = 18
- 2 × 7 = 14
- 3 × 7 = 21
- 2 × 3 × 7 = 42
- 3 × 3 × 7 = 63
- 2 × 3 × 3 × 7 = 126
Therefore, the complete set of factors of 126 is: 1, 2, 3, 6, 7, 9, 14, 18, 21, 42, 63, and 126.
Beyond the Numbers: The Significance of Factors
While the process of finding factors might seem purely mathematical, it has far-reaching implications across various disciplines.
Greatest Common Divisor (GCD): Harmony in Multiplicity
The greatest common divisor (GCD) of two or more numbers is the largest number that divides into all of them. Understanding factors is crucial for finding the GCD. For instance, let’s find the GCD of 126 and 180.
- Prime factorization of 180 = 2 × 2 × 3 × 3 × 5
Comparing the prime factors of 126 and 180, we identify the common prime factors: 2, 3, and 3. Multiplying these common factors together gives us the GCD: 2 × 3 × 3 = 18.
Least Common Multiple (LCM): Finding the Rhythm of Togetherness
The least common multiple (LCM) of two or more numbers is the smallest number that is divisible by all of them. Factors are also essential for determining the LCM. Consider finding the LCM of 126 and 180.
- Prime factorization of 126 = 2 × 3 × 3 × 7
- Prime factorization of 180 = 2 × 2 × 3 × 3 × 5
To find the LCM, we take the highest power of each prime factor that appears in the prime factorizations of both numbers: 22 × 32 × 5 × 7 = 1260. This shows how factors help us understand the relationships between numbers and find their common ground.
Factors in Action: Unlocking Real-World Applications
The concept of factors doesn’t just exist in textbooks; it permeates our everyday lives.
Scheduling and Synchronization: Factors in Motion
Imagine planning a meeting with several people. You need to find a time that works for everyone’s schedules. The LCM can help! For example, if person A is available every 3 days, person B every 4 days, and person C every 6 days, the LCM of 3, 4, and 6 is 12. This means they can all meet every 12 days. Factors help synchronize our actions and create shared experiences.
Cryptography: Keeping Secrets Safe
Cryptography, the art of secure communication, heavily relies on prime numbers and factorization. Encryption algorithms use prime numbers to create complex codes that are incredibly difficult to break without the proper key. This key is often derived from the prime factorization of a large number. Factors play a vital role in protecting sensitive data from unauthorized access.
Factors Of 126
The Intriguing World of Factors: A Continuous Exploration
Our exploration of the factors of 126 has revealed the fascinating world of number theory and its practical applications. We’ve seen how understanding factors can help us unlock the secrets of numbers, find commonalities, and even secure our information. As you delve deeper into the mathematical universe, remember that factors are the building blocks that shape the intricate patterns and relationships between numbers.
This journey is far from over. There are countless numbers waiting to be explored, each harboring a unique set of factors. Continue your own exploration, and you might discover hidden connections, new applications, and an ever-deepening appreciation for the captivating world of mathematics.






