Have you ever stopped to consider the building blocks of numbers? It’s a fascinating journey into the world of factors and multiples, a journey that can be surprisingly engaging. Today, we’re going to explore the factors of 900, unraveling the secrets behind this seemingly ordinary number. This exploration will take us beyond simple arithmetic, revealing patterns and connections that illuminate the beauty of mathematics.
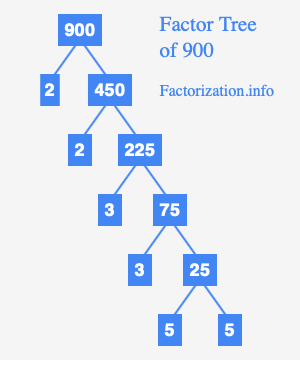
Image: factorization.info
While I was playing a board game with my friends recently, we came across a situation where needing to find the factors of a large number was crucial for strategic decision-making. This made me realize how often we encounter factors in our daily lives, whether it’s during shopping, cooking, or even while playing games. So, let’s dive into the world of factors of 900 and see what wonders await us!
Discovering the Factors of 900
In essence, a factor of a number is a whole number that divides evenly into that number. Think of it as finding the pieces that make up the whole. The factors of 900 are all the numbers that can be multiplied by another whole number to produce 900. For instance, 1 and 900 are factors of 900 because 1 * 900 = 900. Similarly, 2 and 450 are factors because 2 * 450 = 900.
Finding all the factors of 900 involves a systematic approach. One method is to start by dividing 900 by the smallest prime number, which is 2. We find that 900 is divisible by 2, giving us 450. We can continue dividing 450 by 2, which gives us 225. 225 is not divisible by 2, but it is divisible by 3. Continuing this process, we find the factors of 900 are: 1, 2, 3, 4, 5, 6, 9, 10, 12, 15, 18, 20, 25, 30, 36, 45, 50, 60, 75, 90, 100, 150, 180, 225, 300, 450, and 900.
The Role of Prime Factorization
To better understand the factors of 900, we can use a powerful tool called prime factorization. Prime factorization breaks down a number into its prime factors, which are numbers greater than 1 that are only divisible by 1 and themselves. The prime factorization of 900 is 2² * 3² * 5². This means that 900 can be expressed as the product of 2, 3, and 5 raised to certain powers.
This factorization helps us find all the factors of 900 systematically. To obtain a factor, we can take each prime factor and raise it to a power between zero and the power it appears in the prime factorization. For example, taking 2 to the power of 0, 1, and 2 (0 ≤ 2 ≤ 2), we get 1, 2, and 4. Similarly, for 3, we get 1, 3, and 9. And for 5, we get 1, 5, and 25. To find all the factors, we multiply the different combinations of these prime factors.
Exploring the Relationship between Factors and Divisibility Rules
Factors and divisibility rules are closely intertwined. Divisibility rules provide us with shortcuts to determine if a number is divisible by another number without actually performing the division. For example, a number is divisible by 2 if its unit digit is even.
Understanding these divisibility rules can help us find the factors more efficiently. For instance, knowing that 900 is divisible by 2 (its unit digit is even) tells us that 2 is a factor of 900. Similarly, since 900 is divisible by 3 (the sum of its digits, 9, is divisible by 3), we know 3 is a factor. These rules streamline the process of finding the factors, making it less tedious.
Image: www.cuemath.com
Beyond the Basics: Factors and Advanced Concepts
The concept of factors extends beyond just finding the pieces of a number. It plays a vital role in various areas of mathematics:
- Greatest Common Factor (GCD): The GCD of two or more numbers is the largest number that divides into all of them evenly. For instance, the GCD of 12 and 18 is 6.
- Least Common Multiple (LCM): The LCM of two or more numbers is the smallest number that is divisible by all of them. The LCM of 12 and 18 is 36.
- Number Theory: Factors are fundamental to number theory, a branch of mathematics that explores the properties of integers.
- Cryptology: Factors are used in cryptography for encryption and decryption, making data secure.
Exploring these advanced concepts provides a deeper understanding of the role factors play in mathematics and beyond.
Tips and Expert Advice: Mastering the Art of Finding Factors
Here are some tips to help you confidently find the factors of a number:
Finding factors is a foundational skill in mathematics, and it doesn’t have to be daunting. By understanding the concepts and applying the tips mentioned above, you can master this skill and confidently tackle any number-related challenge.
Frequently Asked Questions
Q: What is the difference between a factor and a multiple?
A: A factor is a number that divides evenly into another number, while a multiple is a number that is obtained by multiplying another number by a whole number. For example, the factors of 12 are 1, 2, 3, 4, 6, and 12. The multiples of 12 are 12, 24, 36, 48, and so on.
Q: Why is finding factors important?
A: Finding factors is essential in various areas of mathematics, including arithmetic, algebra, and number theory. It helps us understand the relationships between numbers and makes solving problems more efficient.
Q: Are there any other methods for finding factors?
A: Yes, besides prime factorization, other methods for finding factors include using factor trees, looking for pairs of factors, and using a calculator to divide the number by potential factors.
Q: Can a number have an infinite number of factors?
A: No, a number can only have a finite number of factors because there are only finitely many whole numbers that can divide into a given number evenly.
Factors Of 900
Conclusion
Understanding the factors of 900 has taken us on a journey through the fascinating world of number theory. We learned about prime factorization, divisibility rules, and the broader implications of factors in various mathematical concepts.
Are you interested in exploring the world of factors further? Perhaps you’d like to learn more about the factors of other numbers or delve deeper into number theory? This journey into the realm of factors is just the beginning – there are countless wonders awaiting discovery!






