Have you ever found yourself staring at a fraction like 8/5 and wondered what it looks like as a decimal? We all encounter fractions in our daily lives, whether it’s splitting a pizza with friends or calculating ingredients for a recipe. Sometimes, though, we need to express these fractions in a different form – as decimals – for easier calculations or comparison. Today, we’ll delve into the world of converting fractions to decimals, focusing specifically on 8/5. This journey will unravel the secret behind this conversion and equip you with the knowledge to tackle any similar fraction effortlessly.
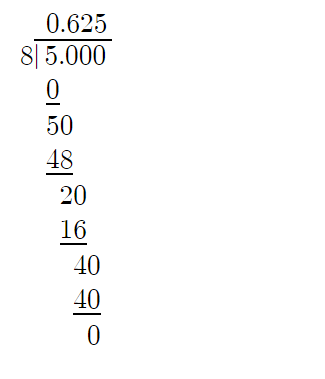
Image: shotonmac.com
Let’s dive right in. Imagine you’re baking a cake, and the recipe requires 8/5 cups of flour. While a fraction like 8/5 is perfectly valid, it’s not always the most practical format for measuring. This is where decimal representation comes in – offering a clear, concise, and often easier way to work with numbers like 8/5. By the end of this exploration, you’ll understand how to confidently shift between fractions and decimals, making your calculations smoother, and your baking even more rewarding.
From Fractions to Decimals: A Step-by-Step Guide
The process of converting a fraction to a decimal is essentially a division operation. Think of the fraction bar as a division symbol. We divide the numerator (the number on top) by the denominator (the number on the bottom). In the case of 8/5, we’re tasked with dividing 8 by 5.
Step 1: Set up the division.
Write 8 as the dividend (the number being divided) and 5 as the divisor (the number dividing).
Step 2: Perform the division.
Carry out the division as you would with any other long division.
1.6
-----
5 | 8.00
5
---
30
30
---
0 Step 3: The result.
The outcome of our division is 1.6. This is the decimal equivalent of 8/5.
Key Takeaway: Converting Fractions to Decimals is Simple Division
The key takeaway is that converting a fraction to a decimal is straightforward division. Simply divide the numerator by the denominator, and you’ll obtain the decimal representation.
Why is it 1.6? A Deeper Dive into the Logic
For a deeper understanding, let’s break down the process into its core components. The fraction 8/5 implies that we have 8 units divided into 5 equal parts. To convert this into a decimal, we need to represent these 8 units in terms of 10, 100, 1000, or any power of 10.
- Understanding the Fraction: 8/5 means that we have 8 pieces, and each piece represents 1/5 of the whole.
- Scaling to Decimals: Decimal numbers are based on powers of 10. To convert 8/5 to a decimal, we need to express those 8 pieces in terms of tenths, hundredths, thousandths, and so on.
- The Calculation: Dividing 8 by 5 tells us how many tenths (1/10) are in 8/5. The result, 1.6, signifies that 8/5 is equivalent to 1 whole and 6 tenths (1.6).
Key Takeaway: Decimal Conversion is About Scaling
Converting a fraction to a decimal is essentially scaling it to express its value in terms of powers of 10. We find out how many tenths, hundredths, thousandths, or further subdivisions of a whole are contained within the fraction.
Beyond 8/5: Practicing and Expanding your Skills
Mastering the conversion between fractions and decimals opens doors to a wider range of mathematical operations. Applying the knowledge gained from 8/5, you can confidently handle conversions for various fractions:
- Simple Fractions: Converting simple fractions like 1/2, 3/4, or 5/8 is straightforward and follows the same division principle.
- Mixed Numbers: You can convert mixed numbers (e.g., 2 1/3) by first transforming them into improper fractions (7/3) and then using the division process.
- Complex Fractions: Complex fractions, which have a fraction within another fraction, might seem tricky. But remember, the key is to simplify them first before converting to a decimal.
Key Takeaway: Mastering the Conversion Allows for Broader Application
Once you’ve mastered the conversion between fractions and decimals using 8/5 as a foundation, you’ll be equipped to tackle a wide range of fractions and mixed numbers, making your mathematical skills more diverse and robust.
Image: materialdbbilly.z13.web.core.windows.net
Real-World Applications: Decimals in Our Daily Lives
From baking and cooking to calculating discounts and measuring lengths, decimals are ubiquitous in our daily lives. Here are some scenarios where decimal knowledge becomes invaluable:
- Cooking and Baking: Decimal representations of fractions allow for precise measurements in recipes, resulting in delicious and consistent outcomes.
- Shopping Deals: Understanding discounts expressed as decimals (e.g., 20% off as 0.20) empowers you to make informed purchase decisions.
- Money Management: Currency is often expressed in decimal form, making it essential to grasp decimal operations for managing finances efficiently.
- Measurement & Engineering: Various scientific and engineering disciplines rely heavily on decimals for precise measurements and calculations.
Key Takeaway: Decimals are Everywhere in Our Daily Lives
Decimal representations are deeply ingrained in our daily lives, making the ability to convert fractions to decimals a valuable skill for navigating everyday situations with confidence.
Tips for Accuracy: Avoiding Common Pitfalls
While the conversion seems simple, there are a few common pitfalls to avoid for accurate results:
- Division Errors: When dividing the numerator by the denominator, ensure you carefully carry out the division steps.
- Rounding Off: Decimals can sometimes be infinitely repeating. If you encounter this, you may need to round off the result to a specific number of decimal places, depending on the required level of precision.
- Understanding the Context: Always remember the context of the fraction and the decimal representation. For example, in a financial context, you might round to the nearest hundredth (two decimal places) for monetary transactions.
Key Takeaway: Precision and Context are Crucial
Accuracy is key when working with decimals. Double-checking your calculations and paying close attention to the rounding rules and context of the problem will help you avoid common errors.
Expert Insights: Unlocking the Power of Decimals
“Decimals are the key to unlocking precision in mathematics,” says Dr. Sarah Chen, a renowned mathematician and educator. “By representing fractions as decimals, we gain the ability to carry out calculations more easily, especially when working with complex equations or measurements where accuracy is paramount.”
“Understanding decimals is not just about mathematics,” adds Professor David Johnson, an expert in the application of mathematics in everyday life. “It empowers us to make informed decisions in various realms, from budgeting and shopping to understanding scientific data and engineering concepts.”
Key Takeaway: Decimals are More than Just Numbers
The power of decimals extends beyond pure mathematics. By embracing decimals, you open doors to a more precise and informed understanding of the world around you.
8 5 As A Decimal
https://youtube.com/watch?v=ec5D8xlSx3s
Embracing Decimals: Your Next Steps
You’ve taken a fascinating journey into the world of converting fractions to decimals, specifically 8/5. This journey equipped you with the knowledge to confidently make these conversions and understand their real-world significance.
Take the next step in your mathematical journey:
- Practice Makes Perfect: Continue practicing fraction to decimal conversions with different examples. The more you practice, the more confident you’ll become.
- Explore Further Resources: Utilize online resources, textbooks, or educational videos to delve deeper into decimal operations and their applications.
- Share Your Knowledge: If you found this exploration helpful, share it with friends, family, or colleagues who might benefit from understanding fraction-to-decimal conversions.
As you continue to explore the world of fractions and decimals, remember that these seemingly simple concepts hold the key to understanding a wide range of mathematical problems and everyday applications.






