Have you ever wondered about the hidden relationships between numbers? The concept of the greatest common factor, or GCF, delves into the very essence of how numbers connect and intertwine. While it might seem like a simple mathematical concept, the GCF plays a crucial role in various areas of mathematics, from simplifying fractions to solving complex equations. To understand the significance of the GCF, let’s embark on a journey to unravel the mystery behind the GCF of 30 and 54.

Image: lessonmediadurr.z21.web.core.windows.net
Finding the GCF of 30 and 54 might initially seem like a straightforward calculation, but it opens up a world of possibilities. By learning how to determine the GCF, we unveil the building blocks of these numbers, uncovering their shared factors and gaining deeper insights into their characteristics. This journey will delve into the fascinating world of prime factorization, explore the historical roots of the GCF, and reveal how this seemingly simple concept has a profound impact on our understanding of numbers.
Exploring the Concept of GCF
Before diving into the specific case of 30 and 54, let’s lay a solid foundation by understanding what the GCF actually is. Put simply, the greatest common factor (GCF) of two or more numbers is the largest number that divides evenly into all of them. Think of it like finding the biggest brick that fits perfectly into two walls, each made up of smaller bricks.
Methods for Finding the GCF
There are several widely used methods for determining the GCF. The most common methods include:
- Listing Factors: This method involves listing out all the factors (numbers that divide evenly) of each number and then identifying the largest common factor.
- Prime Factorization: In this approach, we break down each number into its prime factors (prime numbers that multiply to give the original number). The GCF is found by identifying the prime factors that are common to both numbers and multiplying them together.
- Euclidean Algorithm: This elegant method uses repeated division to efficiently find the GCF. It is particularly helpful for large numbers and offers a more streamlined approach compared to listing factors or prime factorization.
Determining the GCF of 30 and 54
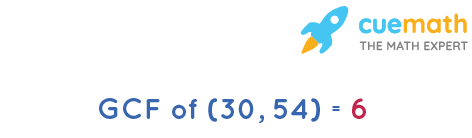
Image: www.cuemath.com
Listing Factors
To find the GCF of 30 and 54 using the listing factors method, we first list out all the factors of each number:
- Factors of 30: 1, 2, 3, 5, 6, 10, 15, 30
- Factors of 54: 1, 2, 3, 6, 9, 18, 27, 54
Next, we identify the largest common factor:
- The common factors of 30 and 54 are 1, 2, 3, and 6.
- The greatest common factor (GCF) is 6.
This method works well for smaller numbers but can become cumbersome for larger numbers.
Prime Factorization
Now, let’s try prime factorization to find the GCF of 30 and 54:
- Prime factorization of 30: 2 x 3 x 5
- Prime factorization of 54: 2 x 3 x 3 x 3
We identify the common prime factors: 2 and 3. We only take the lowest power of each shared prime factor. In this case, both numbers have a single factor of 2 and a single factor of 3.
Multiplying these together, we get: 2 x 3 = 6.
Therefore, the GCF of 30 and 54 is 6.
Euclidean Algorithm
The Euclidean Algorithm provides a more efficient method for finding the GCF. Here’s how it works:
- Divide the larger number by the smaller number: 54 ÷ 30 = 1 (remainder 24)
- Replace the larger number with the smaller number, and the smaller number with the remainder: 30 ÷ 24 = 1 (remainder 6)
- Repeat steps 1 and 2 until the remainder is 0: 24 ÷ 6 = 4 (remainder 0)
Once we have a remainder of 0, the last non-zero remainder (6) is the GCF.
Therefore, the GCF of 30 and 54 is 6.
Real-World Applications of the GCF
The GCF is not just a theoretical mathematical concept; it finds practical applications in various realms of life:
- Simplifying Fractions: The GCF plays a crucial role in simplifying fractions. Dividing the numerator and denominator of a fraction by their GCF reduces the fraction to its simplest form. This simplifies calculations and makes it easier to understand the relationship between the numerator and denominator.
- Dividing Objects Equally: Imagine you have 30 candies and 54 cookies. To divide them equally among the maximum number of people, you need to find the GCF of 30 and 54, which is 6. You can distribute the candies and cookies in 6 groups, with each group receiving 5 candies and 9 cookies.
- Pattern Recognition: The GCF also helps us understand patterns and regularities in numbers. When we find the GCF of two numbers, we identify the common factors that contribute to their characteristics. This recognition of patterns can aid in solving mathematical problems and unraveling complex mathematical relationships.
- Music Composition: The GCF is utilized in music composition to create harmonious intervals and chords. By understanding the GCF of different musical notes, composers can create melodies that are pleasing to the ear.
Gcf Of 30 And 54
Conclusion
Understanding the GCF of 30 and 54 goes beyond a simple calculation; it opens up a gateway into the fundamental nature of numbers. The concepts of prime factorization, factor listing, and the Euclidean Algorithm not only provide us with a toolkit for finding the GCF but also offer valuable insights into the structure and properties of numbers. From simplifying fractions to recognizing patterns, the GCF finds practical applications in various aspects of our lives and serves as a cornerstone of mathematical understanding. The next time you encounter a pair of numbers, remember the concept of the GCF and explore the hidden relationships that lie beneath the surface.






