Ever wondered how architects design buildings with perfectly aligned walls, or how engineers ensure that bridges remain stable? The answer lies in the fundamental principles of geometry, specifically, the fascinating relationship between parallel lines. One of the key concepts that unlocks this relationship is the Consecutive Angle Theorem, a theorem that dictates the specific angles formed when a transversal line intersects two parallel lines.
Image: www.coursehero.com
This article will delve into the world of the Consecutive Angle Theorem, exploring its definition, its historical significance, and its remarkable applications in various fields. We’ll unveil its power in understanding the geometry of parallel lines and how it helps us comprehend and predict the behavior of objects in the real world.
Defining the Consecutive Angle Theorem
The Consecutive Angle Theorem is a cornerstone in the study of parallel lines. It states that **when a transversal line intersects two parallel lines, the consecutive interior angles on the same side of the transversal are supplementary**, meaning that their sum equals 180 degrees. This theorem, along with its close relative, the Alternate Interior Angle Theorem, forms the foundation for numerous geometric calculations and architectural designs.
To understand this theorem better, let’s visualize it: Imagine two parallel lines, line l and line m, intersected by a transversal line, line t. Now, consider two angles formed on the same side of the transversal, one on the interior of line l and the other on the interior of line m. These two angles are deemed consecutive interior angles. The Consecutive Angle Theorem states that the sum of these two angles is always 180 degrees.
The Historical Significance of the Consecutive Angle Theorem
The Consecutive Angle Theorem, along with other geometric theorems related to parallel lines, has been a subject of intense study since ancient times. Early civilizations, particularly the Greeks, recognized the significance of these geometric principles in various practical applications, including architecture, engineering, and surveying. Early Greek mathematicians, such as Euclid, documented the Consecutive Angle Theorem and its relationship to other foundational geometric concepts in his groundbreaking work, “Elements,” a text that remained the foundation of geometry for centuries.
The development of these theorems was crucial for advancing our understanding of space, shapes, and the relationships between them. Their impact extends beyond pure mathematics, influencing fields ranging from mapmaking to the design of spacecraft.
Applications of the Consecutive Angle Theorem
The Consecutive Angle Theorem finds diverse applications in various fields, with its influence extending well beyond the realm of academia. Here are some compelling examples:
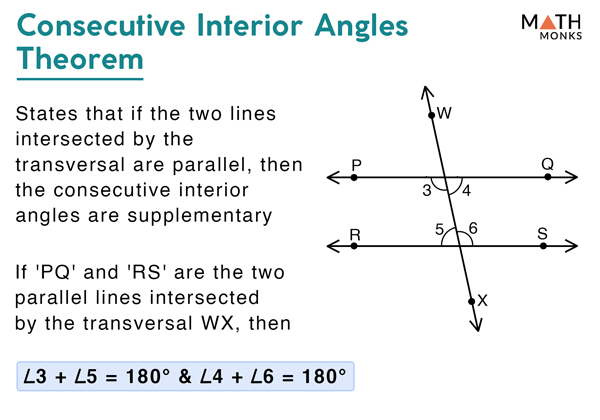
Image: ar.inspiredpencil.com
1. Architecture and Engineering
Architects rely on geometric principles, including the Consecutive Angle Theorem, to ensure the stability and functional integrity of their designs. The theorem allows them to accurately determine the angles of walls, beams, and other structural elements in buildings, ensuring they align perfectly. This principle is essential for constructing visually appealing and structurally sound structures, minimizing the risk of collapse or distortion.
2. Civil Engineering and Road Construction
Civil engineers utilize the Consecutive Angle Theorem extensively for road construction. They ensure that roads are built with consistent angles, facilitating smooth transitions and minimizing the risk of accidents. This principle guarantees roads maintain their alignment, crucial for traffic flow and safety. Furthermore, the theorem helps engineers to design bridges and other infrastructure projects where parallel lines play a critical role.
3. Surveying and Navigation
Surveyors utilize the Consecutive Angle Theorem in their work of accurately measuring land and constructing maps. By applying the principles of parallel lines and the Consecutive Angle Theorem, they can precisely determine the distance between points, the angles of boundaries, and the overall shape of a land parcel. This information is then used to create accurate maps and conduct precise land measurements – essential for various applications like property ownership, urban planning, and infrastructure development.
Understanding the Consecutive Angle Theorem through Real-World Examples
Let’s explore some real-world examples to illustrate how the Consecutive Angle Theorem comes into play:
1. Building a Pergola
Imagine building a pergola with two parallel beams, both at an angle to the ground. A transversal beam connects the two parallel beams, forming consecutive interior angles at the points of intersection. The Consecutive Angle Theorem ensures that the sum of these consecutive interior angles is 180 degrees, guaranteeing the pergola’s structural stability and aesthetic appeal.
2. Constructing a Parallel Parking Space
The Consecutive Angle Theorem also comes into play when designing parallel parking spaces, allowing engineers to ensure that cars park at the correct angle, ensuring a safe and efficient use of parking space. The angles formed between the parking space lines and the curb can be accurately determined using the Consecutive Angle Theorem, ensuring smooth and safe parking maneuvers.
New Developments in Parallel Line Geometry
While the Consecutive Angle Theorem has been a cornerstone for centuries, research and theoretical advancements continue to push the boundaries of parallel line geometry. New developments are being made, particularly in complex fields such as non-Euclidean geometries where the concept of parallel lines takes on new interpretations. These advancements have far-reaching implications in advanced mathematics, theoretical physics, and various other scientific fields.
1. Non-Euclidean Geometries
In non-Euclidean geometries, the traditional concept of parallel lines is challenged. Parallel lines can diverge or even converge, depending on the specific geometry’s rules. The study of these non-Euclidean geometries, driven by complex mathematical theories, is essential for understanding the universe at a cosmological scale and exploring the bending of light around massive objects.
2. Advanced Geometric Algorithms
Computer scientists and mathematicians are developing advanced geometric algorithms that leverage the principles of parallel lines and the Consecutive Angle Theorem to solve complex problems in computer graphics, robotics, and computer vision. These algorithms are essential for creating realistic simulations, optimizing robot movement, and improving the precision of image analysis.
1.8.4 Journal Consecutive Angle Theorem
Conclusion
The Consecutive Angle Theorem, a seemingly simple concept, plays a vital role in various fields, from architecture and engineering to surveying and advanced mathematics. Its understanding is critical for appreciating and applying geometric principles in real-world settings. As we continue to explore the universe and its intricate laws, the Consecutive Angle Theorem stands as a testament to the power of geometrical principles in unlocking the secrets of the world around us. By understanding and applying these principles, we can continue to build, design, and invent, shaping our world and pushing the boundaries of human knowledge.






